Fitting data | Jekyll doc theme

Fit data using a library function and then evaluate the fit results.

Introduction

You fit data with the Fitting GUI, which consists of the Fit Editor and the Table of Fits.

The Fit Editor allows you to:

Specify the fit name, the current data set, and the excluded data set.
Explore various fits to the current data set using a library or custom equation, a smoothing spline, or an interpolant.
Override the default fit options such as the coefficient starting values.
Compare fit results including the fitted coefficients and goodness of fit statistics.

The Table of Fits allows you to:

Keep track of all the fits and their data sets for the current session.
Display a summary of the fit results.
Save or delete the fit results.

Data fitting procedure

Begin by fitting the census data to a second degree polynomial. Then continue fitting the data using polynomial equations up to sixth degree, and a single-term exponential equation.

The data fitting procedure follows these general steps:

Press the Fitting button on the Curve Fitting Tool.

The Fitting GUI opens.
Press the New fit button.

Note that this action always defaults to a linear polynomial fit type. You explore new fits at the beginning of your curve fitting session, and when you are exploring different fit types for a given data set.
Select quadratic polynomial from the Polynomial list.

Name the fit “poly2”.
Press the Apply button or select the Immediate apply check box.

The library model, fitted coefficients, and goodness of fit statistics are displayed in the Results area.
Fit the additional library equations.

For fits of a given type (for example, polynomials), use Copy fit instead of New fit since copying a fit retains the current fit type state thereby requiring fewer steps than creating a new fit each time.

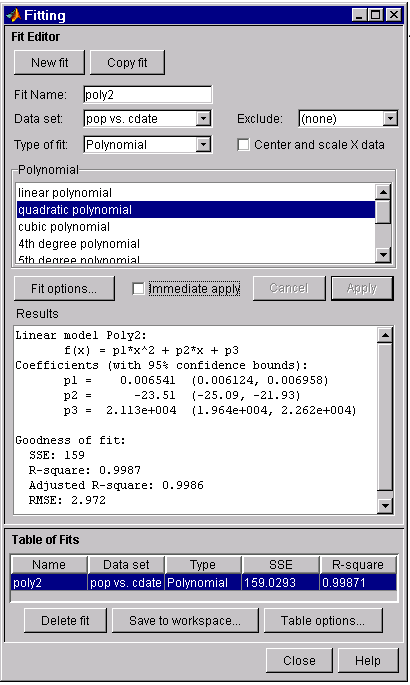
The Fitting GUI is shown below with the results of fitting the census data with a quadratic polynomial.

The data, fit, and residuals are shown below. You display the residuals as a line plot by selecting the menu item View > Residuals > Line plot from the Curve Fitting Tool.

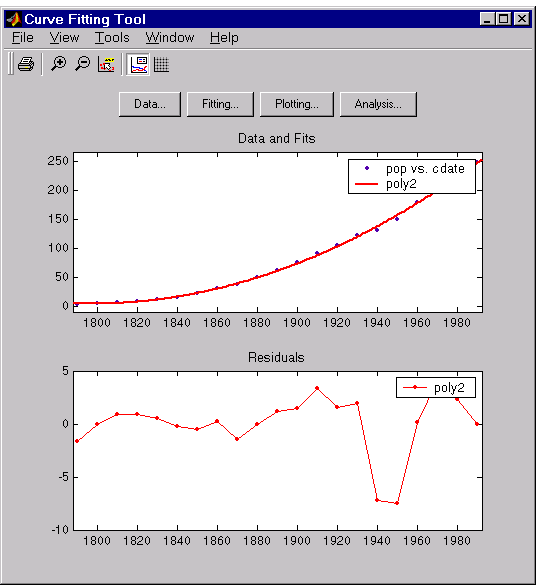
The residuals indicate that a better fit may be possible. Therefore, you should continue fitting the census data following the procedure outlined in the beginning of this section.

Note: The residuals from a good fit should look random with no apparent pattern. A pattern, such as a tendency for consecutive residuals to have the same sign, can be an indication that a better model exists.

When you fit higher degree polynomials, the Results area displays this warning:

Equation is badly conditioned. Remove repeated data points
or try centering and scaling.

The warning occurs because the fitting procedure uses the cdate values as the basis for a matrix with very large values, which results in scaling problems. To address this problem, you can normalize the data. Normalization is a process of scaling the predictor data to improve the accuracy of the subsequent numeric computations. A way to normalize cdate is to center it at zero mean and scale it to unit standard deviation.

(cdate - mean(cdate))./std(cdate)

You normalize data with the Fitting GUI by selecting the Center and scale X data check box.

Note: Since the predictor data changes after normalizing, the values of the fitted coefficients also change when compared to the original data. However, the functional form of the data and the resulting goodness of fit statistics do not change. Additionally, the data is displayed using the original scale.

Determining the best fit

To determine the best fit, you examine both the graphical and numerical fit results.

Graphical fit results

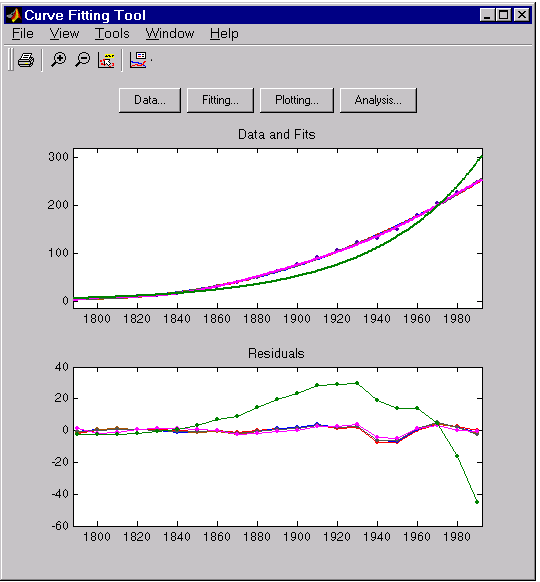
Your initial approach in determining the best fit should be a graphical examination of the fits and residuals. The graphical fit results shown below indicate that:

The fits and residuals for the polynomial equations are all similar making it difficult to choose the best one.
The fit and residuals for the single-term exponential equation indicate it is a poor fit overall. Therefore, it is a poor choice for extrapolation.

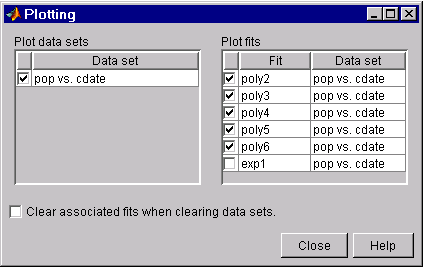
Use the Plotting GUI to remove exp1 from the scatter plot display.

Since the goal of fitting the census data is to extrapolate the best fit to predict future population values, you should explore the behavior of the fits up to the year 2050. You can change the axes limits of the plot by selecting the menu item Tools > Axes Limit Control from the Curve Fitting Tool.

The census data and fits are shown below for an upper abscissa limit of 2050. The behavior of the sixth degree polynomial fit beyond the data range makes it a poor choice for extrapolation.

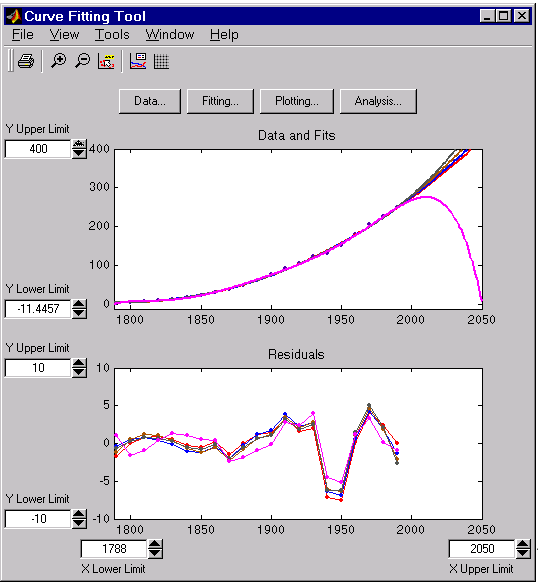
As you can see, you should exercise caution when extrapolating with polynomial fits since they can diverge wildly outside the data range.

Numerical fit results

Since you can no longer eliminate fits by examining them graphically, you should examine the numerical fit results. There are two types of numerical fit results displayed in the Fitting GUI: goodness of fit statistics and confidence intervals on the fitted coefficients. The goodness of fit statistics help you determine how well the curve fits the data. The confidence intervals on the coefficients determine their accuracy.

Some goodness of fit statistics are displayed in the Results area of the Fit Editor for a single fit. All goodness of fit statistics are displayed in the Table of Fits for all fits, which allows for easy comparison.

In this example, the sum of squares due to error (SSE) and the adjusted R-square statistics are used to help determine the best fit. As described in Goodness of Fit Statistics, the SSE statistic is the least squares error of the fit, with a value closer to zero indicating a better fit. The adjusted R-square statistic is generally the best indicator of the fit quality when you add additional coefficients to your model.

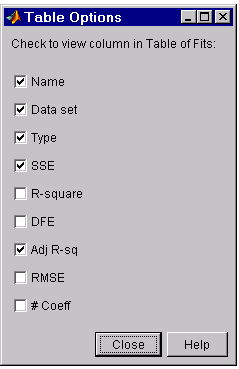
You can modify the information displayed in the Table of Fits with the Table Options GUI. You open this GUI by pressing the Table options button on the Fitting GUI. As shown below, select the adjusted R-square statistic and deselect the R-square statistic.

The numerical fit results are shown below. You can click on the Table of Fits column headings to sort by statistics results.

The SSE for exp1 indicates it is a poor fit, which was already known by examining the fit and residuals. The lowest SSE value is associated with poly6. However, the behavior of this fit beyond the data range makes it a poor choice for extrapolation. The next best SSE value is associated with the fifth degree polynomial fit (poly5) suggesting it may be the best fit. However, the SSE and adjusted R-square values for the remaining polynomial fits are all very close to each other. Which one should you choose?

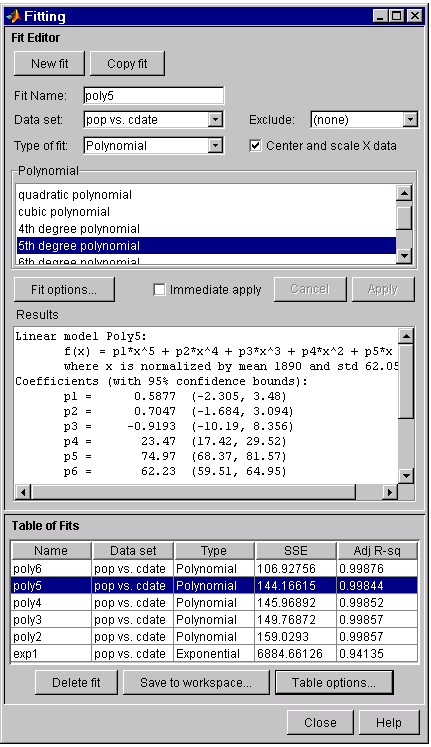
To resolve this issue, examine the confidence bounds for the remaining fits. By default, 95% confidence bounds are calculated. You can change this level by selecting the menu item View > Confidence Level from the Curve Fitting Tool.

The p1, p2, and p3 coefficients for the fifth degree polynomial suggest that it overfits the census data. However, the confidence bounds for the quadratic fit, poly2, indicate that the fitted coefficients are known fairly accurately. Therefore, after examining both the graphical and numerical fit results, it appears that you should use poly2 to extrapolate the census data.

Note: The fitted coefficients associated with the constant, linear, and quadratic terms are nearly identical for each polynomial equation. However, as the polynomial degree increases, the coefficient bounds associated with the higher degree terms indicate that the fitted values are not known accurately, which suggests overfitting.

Saving the fit results

By pressing the Save to workspace button, you can save one or more fits and the associated fit results to the workspace. The fits are saved as an object and the associated fit results are saved as structures. This example saves all the fit results for the best fit, poly2.

fittedmodel is saved as a cfit object:

whos fittedmodel
  Name              Size           Bytes  Class
  fittedmodel       1x1             5038  cfit object
Grand total is 221 elements using 5038 bytes

The cfit object display includes the model, the fitted coefficients, and the confidence bounds for the fitted coefficients:

fittedmodel

fittedmodel =
     Linear model Poly2:
       fittedmodel(x) = p1*x^2 + p2*x + p3
     Coefficients (with 95% confidence bounds):
       p1 =    0.006541  (0.006124, 0.006958)
       p2 =      -23.51  (-25.09, -21.93)
       p3 =  2.113e+004  (1.964e+004, 2.262e+004)

The goodness structure contains goodness of fit results:

goodness

goodness = 
           sse: 159.0293
       rsquare: 0.9987
           dfe: 18
    adjrsquare: 0.9986
          rmse: 2.9724

The output structure contains additional information associated with the fit:

output

output = 
       numobs: 21
     numparam: 3
    residuals: [21x1 double]
     Jacobian: [21x3 double]
     exitflag: 1
    algorithm: 'QR factorization and solve'